Lander | Sequoyah Walters

Report: PDF
Code: LunarLander

Overview

Inspired by the Lunar Lander Atari game, this project aims to perform optimal control on a lander system. Direct collocation is used to obtain an optimal trajectory for the system. Trapezoidal quadrature is used to approximate the various integrals used in the optimal control problem. Finally, Runge-Kutta 4 is used to simulate the dynamics of the system.

Model

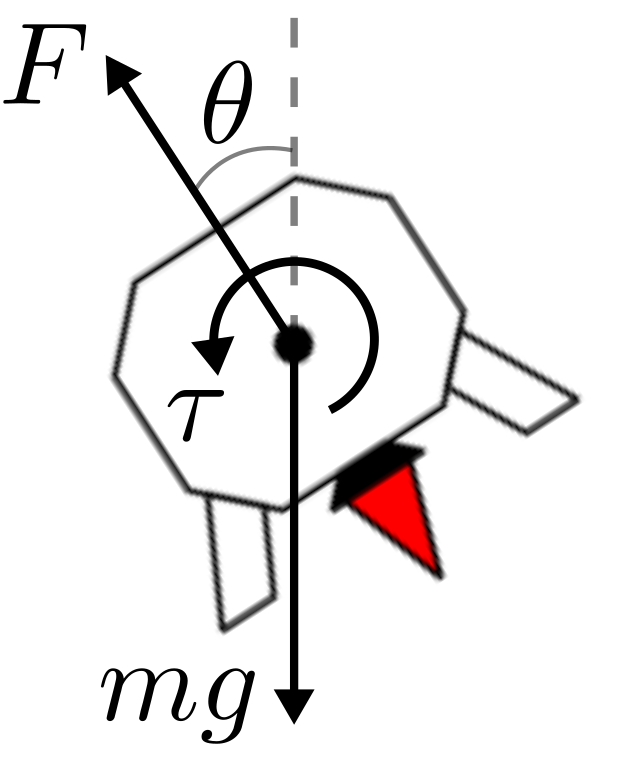
Consider a two-dimensional lander system of mass \(m\) and rotational inertial \(I\) in which thrust \(F\) and torque \(\tau\) are applied as control inputs (see Figure 1). The states of the system include position (\(x\), \(y\)), angle \(\theta\), linear velocity (\(v_x\), \(v_y\)) and angular velocity \(\omega\). Acceleration due to gravity is denoted \(g\), and drag coefficients \(b_v\) and \(b_{\omega}\) scale the drag force and torque, respectively. The system dynamics can then be written as:

\begin{aligned} \dot{x} & = v_{x} \\ \dot{y} & = v_{y} \\ \dot{θ} & = ω \\ {\dot{v}}_{x} & = - \frac{1}{m} (F \sin (θ) + b_{v} v_{x}) \\ {\dot{v}}_{y} & = \frac{1}{m} (F \cos (θ) - b_{v} v_{y}) - g \\ \dot{ω} & = \frac{1}{I} (τ - b_{ω} ω) \end{aligned}

Figure 1: Force diagram of the lander model. Drag not shown.

Optimal Control

To find a sequence of control inputs (thrust, torque) that send the lander from an initial to final desired state, an optimization problem can be solved. This optimization minimizes total “fuel” usage, which equates to minimizing an integral objective function (see the report for more details and math).

Trapezoidal quadrature is used to approximate the integral objective function so direct collocation can be used. The collocation points are points in time, such that each trapezoid is between two collocation points. After solving the optimization, a trajectory of states and control inputs is determined, and can be visualized (see GIF 1).

GIF 1: Optimal trajectory for 3 second front flip in which Earth gravity is used. The initial angle is set to

2 π

and the final angle is set to 0.

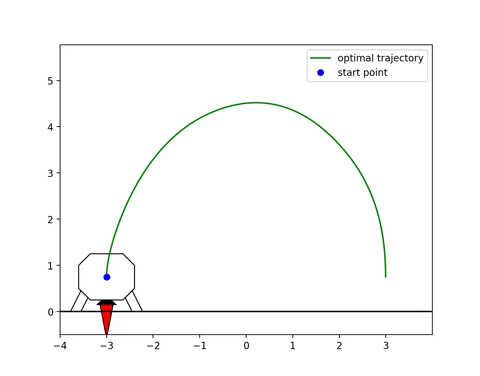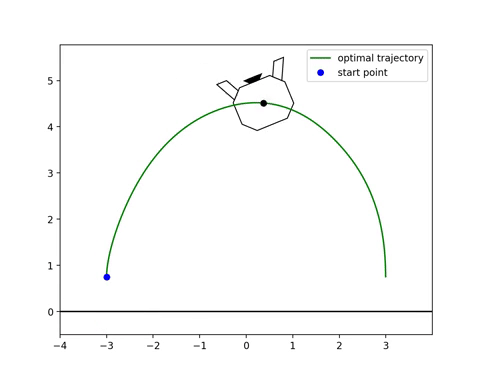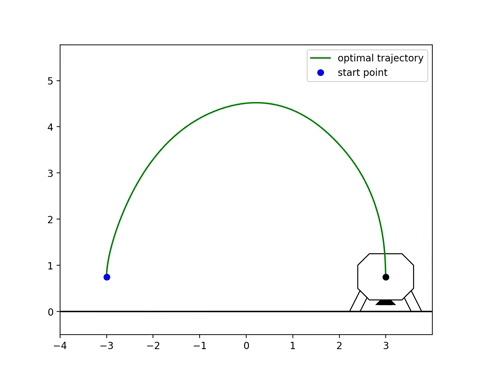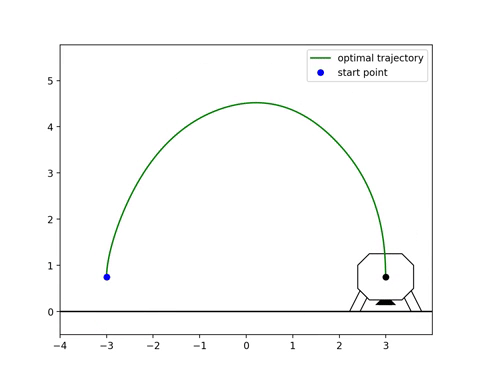
Monte Carlo Simulations

Since the optimal control problem depends on the lander model, uncertainty in the model will cause inaccurate open-loop tracking of the optimal reference trajectory. By using closed-loop control, state feedback is used to augment the optimal control sequence to correct tracking error.

Monte Carlo simulations are used to test how model uncertainty impacts lander flight (same reference trajectory as in GIF 1) when using open-loop and closed-loop control. For each simulation, the drag coefficients are uniformly randomized by \(\pm 5\%\) and mass, gravity and rotational inertia are uniformly randomized by \(\pm 2\%\).

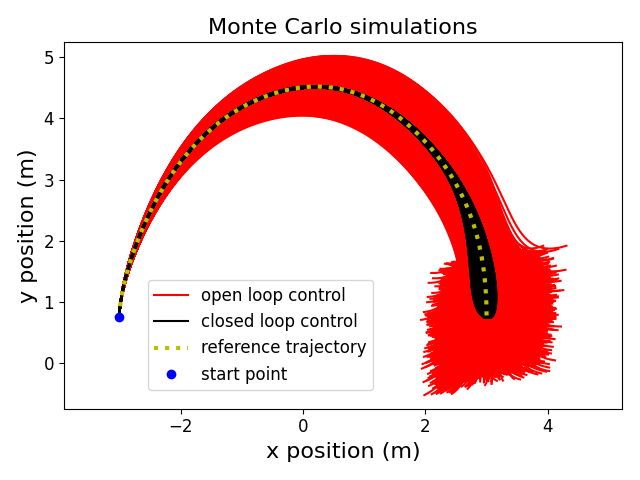
Figure 2: Monte Carlo simulations of lander for open-loop and closed-loop control (10K simulations for each control type).

As shown in Figure 2, the closed-loop controller is able to track the trajectory in the presence of model uncertainty, while the open-loop controller cannot.

Future Directions

Add mountains for the lander to perform obstacle avoidance.
Implement real-time trajectory generation & control for fast reaction to changing environment/objectives.